##############################
## IMPORTS ##
##############################
# greatest common divisor
from math import gcd
# Needed for pi and a few other things
import numpy as np
# For the continued fractions
from fractions import Fraction
# Needed to build the quantum circuit
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
# To simulate running the quantum circuit, transpile any built gates, and
# visualuze the results of the simulation as a histogram
from qiskit_aer import AerSimulator
from qiskit import transpile
from qiskit.visualization import plot_histogram
# Needed to get the inverse QFT
from qiskit.circuit.library import QFTShor’s Factoring Algorithm
This code is modified from the Qiskit Textbook Shor’s Algorithm Code
##############################
## U 7MOD15 ##
##############################
def U_7mod15(power):
"""
Presented withouth proof, this gate is used to factor the number 15
if a = 7.
Inputs:
power (an int): The number of times the gate is to be applied to the
circuit
Returns:
c_U (a qiskit quantum circuit): A controlled version of the U gate needed
by Shor's algorithm
"""
# Define a
a = 7
# This gate will need more than one qubit, in this case the gate needs four qubits
U = QuantumCircuit(4)
# Apply the gate as many times as needed, the gate consists of swapping the four qubits
# and then applying NOT gates
for iteration in range(power):
U.swap(0,1)
U.swap(1,2)
U.swap(2,3)
for q in range(4):
U.x(q)
# Take the finished quantum circuit and make it into a gate
U = U.to_gate()
# Give the circuit a name to be displayed in the circuit diagram
# Note that this can also be accomplished using the name argument in
# the QuantumCircuit functions
U.name = f"{a}^{power} mod 15"
# Make the gate a controlled gate and then return it
c_U = U.control()
return c_U##############################
## CREATE QUANTUM CIRCUIT ##
##############################
# Specify variables
counting_qubits = 8 # number of counting qubits
N = 15 # The number of factor
a = 7 # A number such that 1<a<N and gcd(a,N) = 1
# Create QuantumCircuit with specified counting qubits
# plus 4 qubits for U to act on (the U gate needs 4 qubits)
q = QuantumRegister(counting_qubits + 4)
c = ClassicalRegister(counting_qubits)
qc = QuantumCircuit(q,c)
# Initialize counting qubits
# in state |+>
for q in range(counting_qubits):
qc.h(q)
# And auxiliary register in state |1>
qc.x(counting_qubits)
# Do controlled-U operations
for q in range(counting_qubits):
# Control qubit + Target qubits (the last for qubits)
qc.append(U_7mod15(2**q), [q] + [i+counting_qubits for i in range(4)])
# Do inverse-QFT
qc = qc.compose(QFT(counting_qubits, inverse=True), range(counting_qubits))
# Measure circuit
qc.measure(range(counting_qubits), range(counting_qubits))
# Draw the circuit
qc.draw(output="mpl", fold=-1) # -1 means 'do not fold'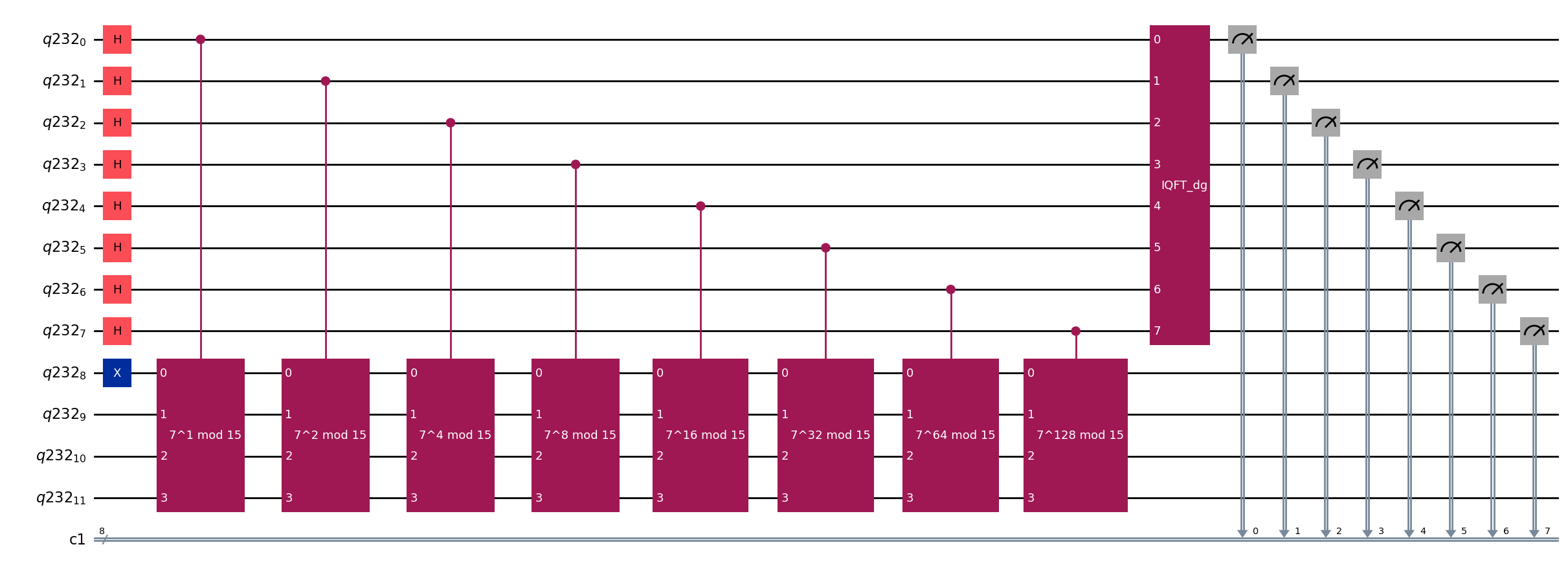
##############################
## SIMULATE QUANTUM CIRCUIT ##
##############################
# Define the simulator, transpile the circuit, simulate the circuit, and then print
# a histogram of the results
aer_sim = AerSimulator()
t_qc = transpile(qc, aer_sim)
results = aer_sim.run(t_qc).result().get_counts()
plot_histogram(results)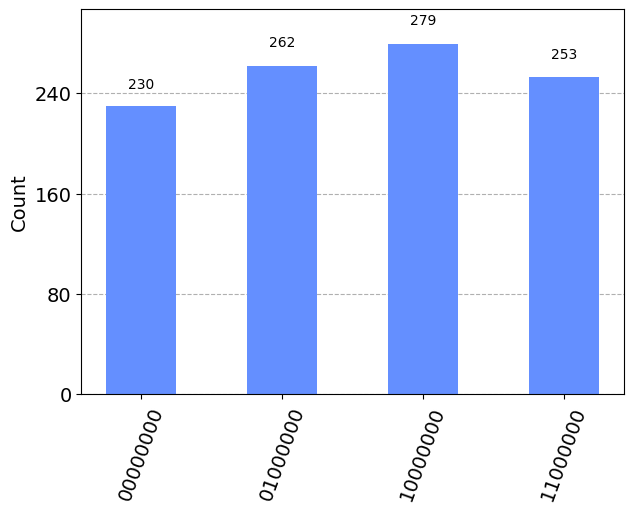
##############################
## CONVERT TO DECIMAL ##
##############################
def convert_to_decimal(b):
"""
Converts a binary string to an decimal using the quantum phase estimation
algorithm
Inputs:
b (a binary string)
Returns:
sum (a float): the binary string converted to a decimal
"""
sum = 0
for i in range(len(b)):
sum += int(b[i])/2**(i+1)
return sum
# Note that unlike previous iterations of this function, we do not want to convert
# the result of the QPE algorithm to an angle, so we do not multiply by 2*pi##########################################
## CONVERT SIMULATION RESULTS TO ANSWER ##
##########################################
# Sort the returned dictionary in order of counts of each result
sorted_results = sorted(results, key=results.get, reverse=True)
# For each possible result, convert it to a decimal
s_over_r_decimal = [convert_to_decimal(i) for i in sorted_results]
# For each possible decimal approximation of s/r, use continued fractions to
# get a more usable representation. Note that the limit_denominator function
# will limit the denomonator of the returned fraction to equal to or below the
# given number (r must be less than 15).
s_over_r = [Fraction(i).limit_denominator(N) for i in s_over_r_decimal]
# Extract the denominator (or r) from all of the fraction approximations to
# s.r
r_guess = [f.denominator for f in s_over_r]
# r must be even, so keep only the even values
r_guess = [r for r in r_guess if r % 2 == 0]
# Define a^(r/2), int because the gcd function must have an int input
a_r_2 = [int(a**(r/2)) for r in r_guess]
# The possible factors of N can be found using a, r, and the gcd function
factor1 = [gcd(num+1,15) for num in a_r_2]
factor2 = [gcd(num-1,15) for num in a_r_2]
# Print the guessed r values as well as the factors found with each r value
# and with each equation
print(r_guess)
print(factor1)
print(factor2)[2, 4, 4]
[1, 5, 5]
[3, 3, 3]