Quantum Key Distribution

##############################
##          IMPORTS         ##
##############################
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit_aer import AerSimulator
import numpy as np
from qiskit.quantum_info import Statevector

A First Attempt

################################
## SEND A MESSAGE WITH NO SPY ##
################################
# Create a message to be passed, in this case the color purple
# Red contributon, green contribution, purple contribution
purple_binary = "10011101" + "00000000" + "11111111"
# Get the length of the string
n = len(purple_binary)

# Create a quantum circuit with one qubit and one bit per digit in 
# the message to be passed
q = QuantumRegister(n)
c = ClassicalRegister(n)
qc = QuantumCircuit(q,c)

# Encode the message in the circuit by adding NOT gates to represent ones
for i in range(n):
    if purple_binary[i] == "1":
        qc.x(i)

# Add Hadamard gates to create a superposition
qc.h(range(n))

# Create a barrier to represent the message being sent
qc.barrier()
statevector = Statevector(qc)
display(statevector.draw(output = 'latex')) 

# Use Hadamard gates to collapse the superposition
qc.h(range(n))

statevector = Statevector(qc)
display(statevector.draw(output = 'latex')) 

# Measure the results of the circuit
qc.measure(range(n), range(n))

# Draw the circuit
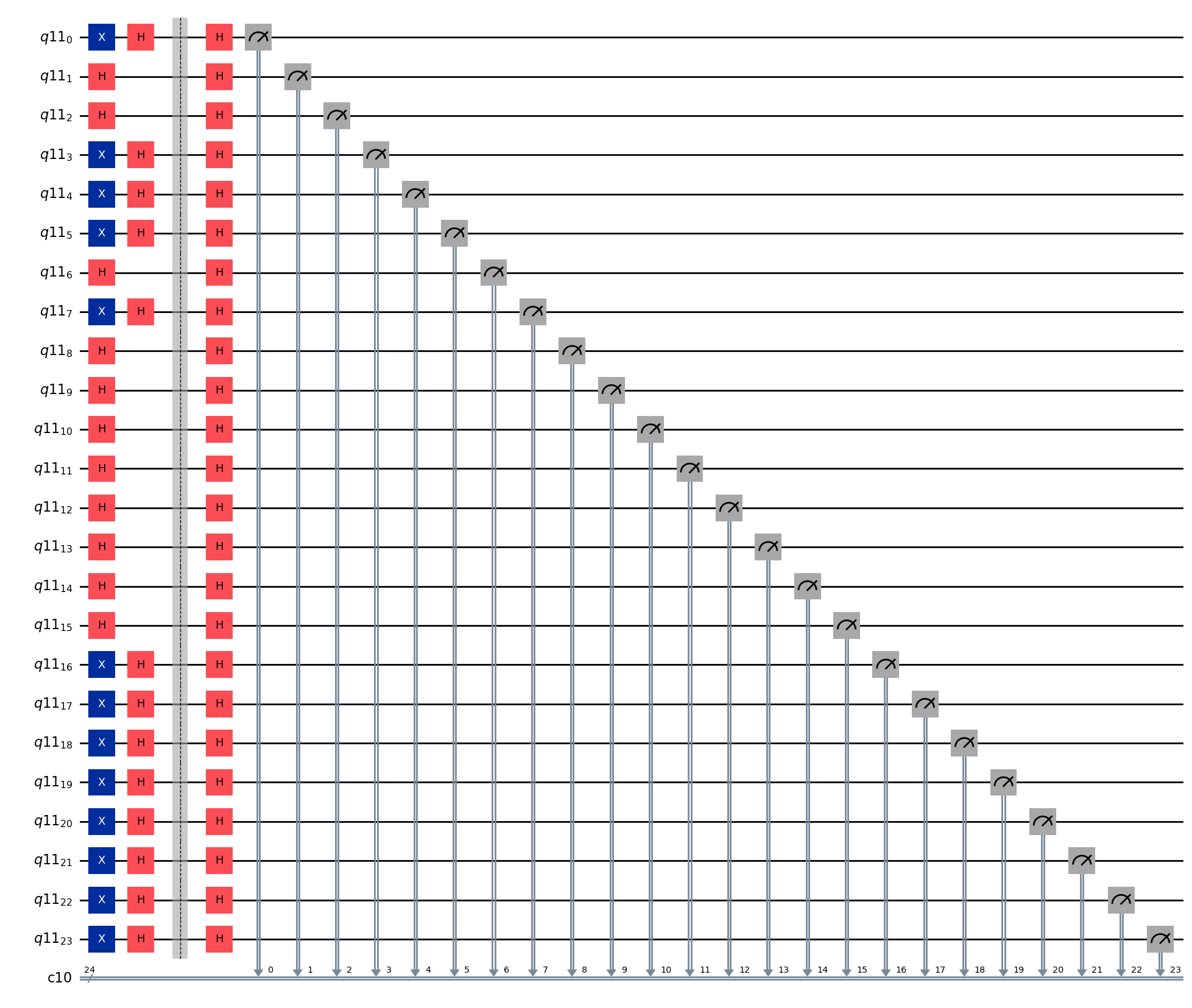
qc.draw(output="mpl", fold=-1)

   

\[0.0002441406 |000000000000000000000000\rangle-0.0002441406 |000000000000000000000001\rangle+0.0002441406 |000000000000000000000010\rangle-0.0002441406 |000000000000000000000011\rangle+0.0002441406 |000000000000000000000100\rangle-0.0002441406 |000000000000000000000101\rangle + \ldots -0.0002441406 |111111111111111111111011\rangle+0.0002441406 |111111111111111111111100\rangle-0.0002441406 |111111111111111111111101\rangle+0.0002441406 |111111111111111111111110\rangle-0.0002441406 |111111111111111111111111\rangle\]

\[ |111111110000000010111001\rangle\]

####################################
## SEND A MESSAGE WITH NO SPY     ##
## SIMULATE RECIEVING THE MESSAGE ##
####################################
# Simulate running the circuit and compare the top result to the secret message
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
# Sort the returned dictionary in order of counts of each result
sorted_results = sorted(results, key=results.get, reverse=True)
print("Number of Results:", len(sorted_results))
print("Messsage Correct?", sorted_results[0][::-1] == purple_binary)

Number of Results: 1
Messsage Correct? True

#############################
## SEND A MESSAGE WITH SPY ##
#############################

# Create a message to be passed, in this case the color purple
# Red contributon, green contribution, purple contribution
purple_binary = "10011101" + "00000000" + "11111111"
# Get the length of the string
n = len(purple_binary)

# Create a quantum circuit with one qubit and one bit per digit in 
# the message to be passed
q = QuantumRegister(n)
c = ClassicalRegister(n)
qc = QuantumCircuit(q,c)

# Encode the message in the circuit by adding NOT gates to represent ones
for i in range(n):
    if purple_binary[i] == "1":
        qc.x(i)

# Add Hadamard gates to create a superposition
qc.h(range(n))

# Create a barrier to represent the message being sent
qc.barrier()

# Assume that someone looks at (measures) the message during transmission
qc.measure(range(4), range(4))
#qc.measure(range(4), range(4))
qc.barrier()

# Use Hadamard gates to collapse the superposition
qc.h(range(n))

#qc.remove_final_measurements()
#statevector = Statevector(qc)
#display(statevector.draw(output = 'latex')) 
print(qc.draw())

# Measure the results of the circuit
qc.measure(range(n), range(n))

# Draw the circuit
qc.draw(output="mpl", fold=-1)

        ┌───┐┌───┐ ░ ┌─┐          ░ ┌───┐
 q17_0: ┤ X ├┤ H ├─░─┤M├──────────░─┤ H ├
        ├───┤└───┘ ░ └╥┘┌─┐       ░ ├───┤
 q17_1: ┤ H ├──────░──╫─┤M├───────░─┤ H ├
        ├───┤      ░  ║ └╥┘┌─┐    ░ ├───┤
 q17_2: ┤ H ├──────░──╫──╫─┤M├────░─┤ H ├
        ├───┤┌───┐ ░  ║  ║ └╥┘┌─┐ ░ ├───┤
 q17_3: ┤ X ├┤ H ├─░──╫──╫──╫─┤M├─░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║ └╥┘ ░ ├───┤
 q17_4: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
 q17_5: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤└───┘ ░  ║  ║  ║  ║  ░ ├───┤
 q17_6: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤┌───┐ ░  ║  ║  ║  ║  ░ ├───┤
 q17_7: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤└───┘ ░  ║  ║  ║  ║  ░ ├───┤
 q17_8: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤      ░  ║  ║  ║  ║  ░ ├───┤
 q17_9: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤      ░  ║  ║  ║  ║  ░ ├───┤
q17_10: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤      ░  ║  ║  ║  ║  ░ ├───┤
q17_11: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤      ░  ║  ║  ║  ║  ░ ├───┤
q17_12: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤      ░  ║  ║  ║  ║  ░ ├───┤
q17_13: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤      ░  ║  ║  ║  ║  ░ ├───┤
q17_14: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤      ░  ║  ║  ║  ║  ░ ├───┤
q17_15: ┤ H ├──────░──╫──╫──╫──╫──░─┤ H ├
        ├───┤┌───┐ ░  ║  ║  ║  ║  ░ ├───┤
q17_16: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
q17_17: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
q17_18: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
q17_19: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
q17_20: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
q17_21: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
q17_22: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        ├───┤├───┤ ░  ║  ║  ║  ║  ░ ├───┤
q17_23: ┤ X ├┤ H ├─░──╫──╫──╫──╫──░─┤ H ├
        └───┘└───┘ ░  ║  ║  ║  ║  ░ └───┘
c16: 24/══════════════╩══╩══╩══╩═════════
                      0  1  2  3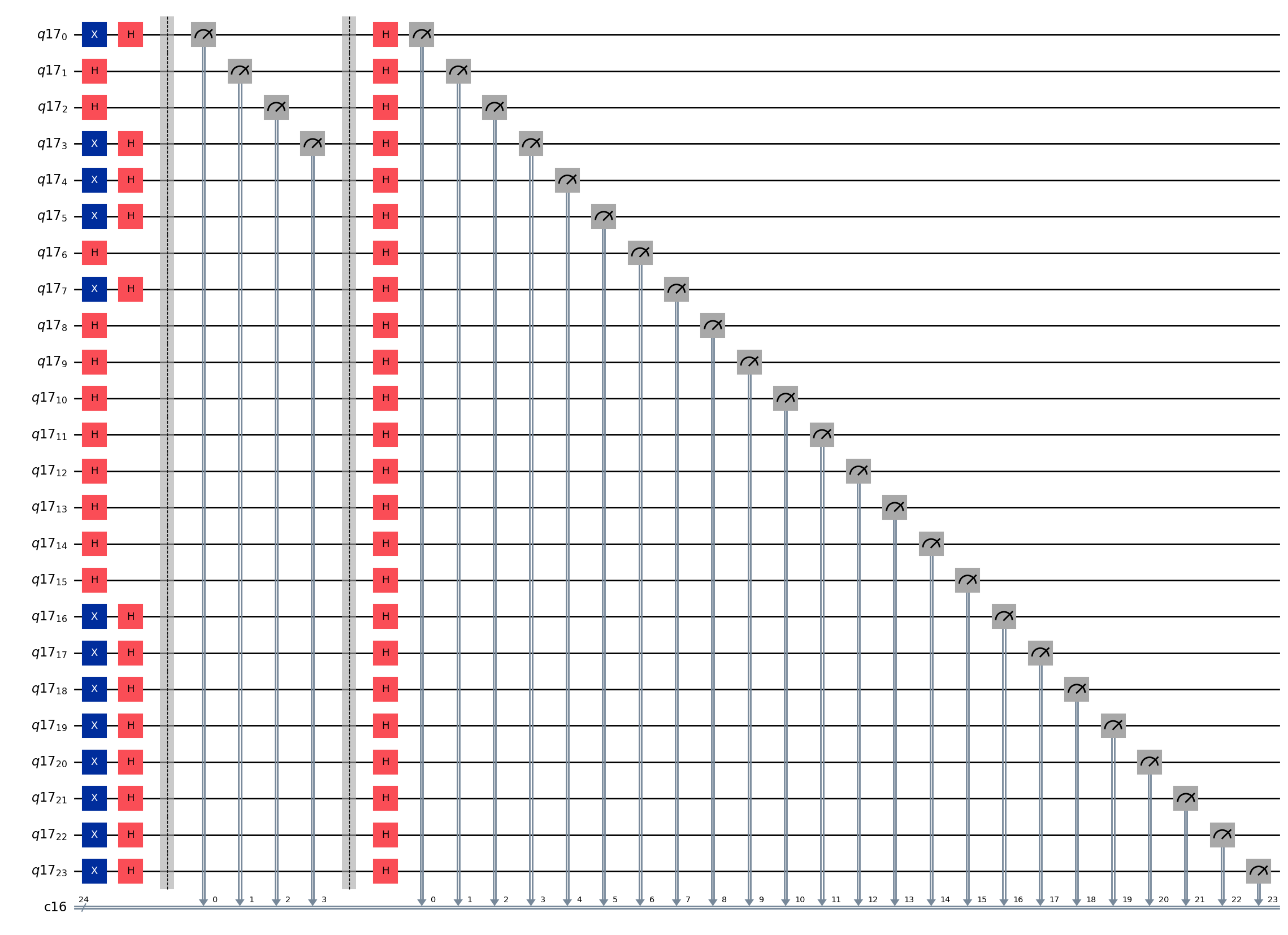         

####################################
## SEND A MESSAGE WITH SPY        ##
## SIMULATE RECIEVING THE MESSAGE ##
####################################
# Simulate running the circuit and compare the top result to the secret message
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
# Sort the returned dictionary in order of counts of each result
sorted_results = sorted(results, key=results.get, reverse=True)
print("Number of Results:", len(sorted_results))
print("Messsage Correct?", sorted_results[0][::-1] == purple_binary)

Number of Results: 16
Messsage Correct? False

A Better Attempt

####################################
##      RANDOM BINARY STRING      ##
####################################
def random_binary_string (n):
    """
        Creates a random binary string (list) of a 
        specified length.
        Inputs:
            n (an int): the length of the binary string
                to be created
        Returns:
            Unnamed (a Numpy Array): the random binary
                string where each digit is a separate 
                element of the array.
    """
    return np.random.randint(2, size=n)

####################################
##               F1               ##
####################################
def F1 (bit):
    """
        Applies the F1 filter to the specified binary
        digit. The F1 filter does not apply any gates
        outside those needed to create the qubit in the
        specified state.
        Inputs:
            bit (an int): a binary digit
        Returns:
            qc (a qiskit circuit): the quantum circuit 
                correspondig to the F1 filter being applied
                to the specified bit.
    """
    if bit == 0:
        q = QuantumRegister(1)
        c = ClassicalRegister(1)
        qc = QuantumCircuit(q,c)
    else:
        q = QuantumRegister(1)
        c = ClassicalRegister(1)
        qc = QuantumCircuit(q,c)
        qc.x(0)
    return qc

####################################
##               F2               ##
####################################
def F2 (bit):
    """
        Applies the F2 filter to the specified binary
        digit. The F2 filter applies a Hadamard gate 
        after the circuit has been created in the specified
        state.
        Inputs:
            bit (an int): a binary digit
        Returns:
            qc (a qiskit circuit): the quantum circuit 
                correspondig to the F2 filter being applied
                to the specified bit.
    """
    if bit == 0:
        q = QuantumRegister(1)
        c = ClassicalRegister(1)
        qc = QuantumCircuit(q,c)
        qc.h(0)
    else:
        q = QuantumRegister(1)
        c = ClassicalRegister(1)
        qc = QuantumCircuit(q,c)
        qc.x(0)
        qc.h(0)
    return qc

####################################
##        RANDOM GATE ORDER       ## 
####################################
def random_gate_order (n):
    """
        Creates a random array of 1's and 2's to
        determine the order the filters (gates)
        should be applied.
        Inputs:
            n (an int): the length of the binary
                string
        Returns:
            Unnamed (a Numpy Array): 1's and 2's which
                are used to determine which filter is 
                applied to which digit in the binary
                string.
    """
    return np.random.randint(2, size=n)+1

####################################
##          APPLY GATES           ##
####################################
def apply_gates(string, gate_order):
    """
        Applies one gate in the gate_order array to the 
        corresponding digit in the the string array. 
        Results in a list of quantum circuits.
        Inputs:
            string (a Numpy array): represents the string
                to be sent
            gate_order (a Numpy array): reprsents the order
                the filters should be applied to the digits
                of the string
        Returns:
            message (a list of qiskit circuits): the quantum
                message to be transmitted.
    """
    message = []
    for i in range(len(string)):
        if gate_order[i] == 1:
            message.append(F1(string[i]))
        else:
            message.append(F2(string[i]))
    return message

####################################
##          UNAPPLY GATES         ##
####################################
def unapply_gates (message, gate_order):
    """
        Decrypts the message sent via quantum key distribution
        using a random order of filters.
        Inputs:
            message (a list of qiskit circuit): The encoded messsage
            gate order (a list): The order to apply the filters to 
                decode the message
        Returns:
            string (a list): The decoded string, where each element of
                the list is a digit in the string
    """
    string = []
    for i in range(len(message)):
        qc = message[i]
        if gate_order[i] == 1:
            qc.measure(0,0)
            results = simulator.run(qc, shots=1).result().get_counts()
            # Sort the returned dictionary in order of counts of each result
            result = sorted(results, key=results.get, reverse=True)[0]
            string.append(result)
        else:
            qc.h(0)
            qc.measure(0,0)
            results = simulator.run(qc, shots=1).result().get_counts()
            # Sort the returned dictionary in order of counts of each result
            result = sorted(results, key=results.get, reverse=True)[0]
            string.append(str(result))
    return string

################################################
## SIMULATE QUANTUM KEY DISTRIBUTION          ##
## ASSUME NO SPY IS WATCHING THE TRANSMISSION ##
################################################
# Define the number of digits to be in the potential secret key
n = 1000
# Define the number of digits to share at the end of the process
share = 100
# String for Person 1
string1 = random_binary_string(n)

# Order of gates to be applied for Person 1
gate_order1 = random_gate_order(n)

# Person 1 creates the message by applying the gates
# to the string of binary digits
message = apply_gates(string1, gate_order1)

# Person 2 chooses which gates to apply to which digit 
# when recieving the secret message
gate_order2 = random_gate_order(n)

# Person 2 uses the random order of gates to decrypt the message
string2 = unapply_gates(message, gate_order2)

# Person 1 and Person 2 compare the order in which they applied 
# the gates. Find the indicies where the gates differ
compare = gate_order1 == gate_order2
remove_indices = np.where(compare==False)[0].tolist()

# If the list of indices to be removed is not empty
# remove the digits at those indices
if remove_indices:
    string1 = np.delete(string1, remove_indices)
    string1 = [str(i) for i in string1]
    string1 = ''.join(string1)
    
    string2 = np.delete(string2, remove_indices)
    string2 = [str(i) for i in string2]
    string2 = ''.join(string2)

# Now compare the digits in the share length. If the shared
# strings match, remove those digits from the string and create
# the secret key. If they do not match then there is a hacker
if string1[:share] == string2[:share]:
    secret_key = string1[share:]
    print(secret_key)
else:
    print("HACKER")
    

111111001010011110000110001110111110000010010100001010110100111100110101000100010010111110100111011001101110011110111010101111101110110000001001111110000101100000110100010100100010010001100011100000100011110000000110110111100101011000011111011011111000000001000111011011010100001100111101011100111000011111000110101111001000010010111111110111011000111001011001000010110011111101111110101101100

#############################################
## SIMULATE QUANTUM KEY DISTRIBUTION       ##
## ASSUME SPY IS WATCHING THE TRANSMISSION ##
## CASE 1: SPY LOOKS AT THE MESSAGE        ##
#############################################
# Define the number of digits to be in the potential secret key
n = 1000
# Define the number of digits to share at the end of the process
share = 100
# String for Person 1
string1 = random_binary_string(n)

# Order of gates to be applied for Person 1
gate_order1 = random_gate_order(n)

# Person 1 creates the message by applying the gates
# to the string of binary digits
message = apply_gates(string1, gate_order1)

# The spy just measures all of the transmitted circuits
# to determine their value
spy_string = []
for m in message:
    m.measure(0,0)
    results = simulator.run(m, shots=1).result().get_counts()
    # Sort the returned dictionary in order of counts of each result
    result = sorted(results, key=results.get, reverse=True)[0]
    spy_string.append(str(result))
    


# Person 2 chooses which gates to apply to which digit 
# when recieving the secret message
gate_order2 = random_gate_order(n)

# Person 2 uses the random order of gates to decrypt the message
string2 = unapply_gates(message, gate_order2)

# Person 1 and Person 2 compare the order in which they applied 
# the gates. Find the indicies where the gates differ
compare = gate_order1 == gate_order2
remove_indices = np.where(compare==False)[0].tolist()

# If the list of indices to be removed is not empty
# remove the digits at those indices
if remove_indices:
    string1 = np.delete(string1, remove_indices)
    string1 = [str(i) for i in string1]
    string1 = ''.join(string1)
    
    string2 = np.delete(string2, remove_indices)
    string2 = [str(i) for i in string2]
    string2 = ''.join(string2)

# Now compare the digits in the share length. If the shared
# strings match, remove those digits from the string and create
# the secret key. If they do not match then there is a hacker
if string1[:share] == string2[:share]:
    secret_key = string1[share:]
    print(secret_key)
else:
    print("HACKER")
    print("SECRET STRINGS DO NOT MATCH")
    

HACKER
SECRET STRINGS DO NOT MATCH