# Needed to set up the quantum circuit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
# Needed to simulate running a quantum computer
from qiskit_aer import AerSimulator
# Neded to visualize the results of running a quantum computer
from qiskit.visualization import plot_histogram
# Needed for vectors and stuff
import numpy as np
def bv_algorithm_alternative (s):
"""
An alternative version of the Berstein-Varirani algorithm which contains
only NOT gates in the oracle
Inputs:
s (a string): the secret string in the oracle that needs to be decoded
Returns:
circuit: a qiskit circuit with the algorithm implemented
"""
# Get the length of the string
n = len(s)
# Need n qubits. n are mapped to the n classical bits
q = QuantumRegister(n)
# Need n classical bits
c = ClassicalRegister(n)
# creates a quantum circuit that maps the result of a qubit
# to a classical bit
circuit = QuantumCircuit(q, c)
circuit.barrier()
# enumerate returns the index and value for each element in the string
# Reversed because of the way qiskit displays the results
# Note though that s is only referenced one time
# The number of queries to s is just 1
for i, bit in enumerate(reversed(s)):
# If the current bit is a one, then add a not gate to that qubit
if bit == '1':
# i is the control qubit, n is the target qubit
circuit.x(i)
circuit.barrier() # just a visual aid for now
# measure the qubits indexed from 0 to n-1 and store them into the
# classical bits indexed 0 to n-1
circuit.measure(range(n), range(n))
# Return the circuit
return circuitSimulating More Complicated Quantum Circuits
Problem 1
An algorithm with the same end result as the Bernstein-Varirani algorithm can be created using an oracle made only of NOT gates. Create this oracle and prove it works by decoding a secret string of length 3, a secret string of length 5, and a secret string of length 7.
# Test the circuit with secret string of length 3, then length 5, and finally length 7
circuit_3 = bv_algorithm_alternative('100')
circuit_5 = bv_algorithm_alternative('10010')
circuit_7 = bv_algorithm_alternative('1001001')# Simulate the circuit, all results should give us the "secret string"
simulator = AerSimulator()
results = simulator.run(circuit_3).result().get_counts()
# Print the secret string and the results of the simulation
print("Known Secret String:", '100')
print("Secret String from Algorithm:", results)Known Secret String: 100
Secret String from Algorithm: {'100': 1024}# Simulate the circuit, all results should give us the "secret string"
simulator = AerSimulator()
results = simulator.run(circuit_5).result().get_counts()
# Print the secret string and the results of the simulation
print("Known Secret String:", '10010')
print("Secret String from Algorithm:", results)Known Secret String: 10010
Secret String from Algorithm: {'10010': 1024}# Simulate the circuit, all results should give us the "secret string"
simulator = AerSimulator()
results = simulator.run(circuit_7).result().get_counts()
# Print the secret string and the results of the simulation
print("Known Secret String:", '1001001')
print("Secret String from Algorithm:", results)Known Secret String: 1001001
Secret String from Algorithm: {'1001001': 1024}Problem 2
Using the quantum Fourier transform algorithm developed in class, create a quantum circuit that will perform a QFT on the following data points. Show the results in terms of Bloch sphere representations. Remember you can use the bin function in Python to convert a number to its binary representation. * x = 5 * x = 10 * x = 21 * x = 35 * x = 2
# This import let's us visualize the Qiskit qubits as state vectors (bra-ket notation)
from qiskit.quantum_info import Statevector
# This import let's us visualize
from qiskit.visualization import plot_bloch_multivector
# Define pi
pi = np.pi
## The below three functions are taken from the code for lecture 10
def qft_rotations(circuit, n):
"""
Performs qft on the first n qubits in circuit (without swaps)
Inputs:
circuit is the qiskit circuit
n is the number of qubits in the circuit
Returns
circuit after adding Hadamard gates and controlled phase gates to perform
the qft
"""
# Break condition
if n == 0:
return circuit
# Subtract 1 because the highest indexed qubit is one less than the total number of qubits
n -= 1
# Hadamard to the highest indexed qubit
circuit.h(n)
# Controlled phase gate with the qubit at n (the highest ordered) being the target and every
# lower indexed qubit being the control in order
for qubit in range(n):
phi = pi/2**(n-qubit)
circuit.cp(phi, qubit, n)
# Recursion time!
# Recall the function with the same circuit, but n is one less than it was originally
# The next run-through will ignore the highest indexed qubit in this run-through
qft_rotations(circuit, n)
def swap_qubits(circuit, n):
"""
Performs swaps the locations of all qubits
Inputs:
circuit is the qiskit circuit
n is the number of qubits in the circuit
Returns
circuit after swapping all qubits
"""
# Int in range function because range requires an integer
for qubit in range(int(n/2)):
# swap the position of a low-indexed qubit and the qubit
# that is the same distance from the highest ordered qubit
circuit.swap(qubit, n-qubit-1)
return circuit
def qft(circuit, n):
"""
Performs QFT on a qiskit circuit by adding the correct gates to the circuit and then
swapping the order of the qubits
Inputs:
circuit is the qiskit circuit
n is the number of qubits in the circuit
Returns:
circuit is the qiskit circuit after the qft gates are applied
"""
qft_rotations(circuit, n)
swap_qubits(circuit, n)
return circuit# Print out the binary form of each number, and then the length of the binary string to see how many qubits
# Remove two from the length of the binary representation to account for the "0b" leading the binary representation
print("Binary Version of 5:", bin(5), "Number of Digits:", len(bin(5))-2)
print("Binary Version of 10:", bin(10), "Number of Digits:", len(bin(10))-2)
print("Binary Version of 10:", bin(21), "Number of Digits:", len(bin(21))-2)
print("Binary Version of 10:", bin(35), "Number of Digits:", len(bin(35))-2)
print("Binary Version of 10:", bin(2), "Number of Digits:", len(bin(2))-2)Binary Version of 5: 0b101 Number of Digits: 3
Binary Version of 10: 0b1010 Number of Digits: 4
Binary Version of 10: 0b10101 Number of Digits: 5
Binary Version of 10: 0b100011 Number of Digits: 6
Binary Version of 10: 0b10 Number of Digits: 2# Create a general function that will work for all the numbers
def qft_on_number (num):
"""
Performs quantum Fourier transform on a number by first converting it
to a binary representation
Inputs:
num (an int): the number to perform the quantum Fourier transform on
Returns:
qc (a Qiskit circuit): the qiskit circuit which will perform the
quantum Fourier transform
"""
# Get the length of the binary number
n = len(bin(num))-2
# Get the binary representation without the leading "0b"
bin_rep = bin(num)[2:]
# Create a quantum circuit that has as many qubits and classical bits as there
# are binary digits in the number
q = QuantumRegister(n)
c = ClassicalRegister(n)
qc = QuantumCircuit(q,c)
# If there is a one in the binary representation then add a not gate to the corresponding
# qubit
# Reverse the binary representation before doing this for the same reasons as it is done
# for the BV algorithm
for i, bit in enumerate(reversed(bin_rep)):
# If the current bit is a one, then add a not gate to that qubit
if bit == '1':
# i is the control qubit, n is the target qubit
qc.x(i)
# Measure and simulate the algorithm just to ensure we have the correct output
qc.measure(q,c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
print(num, "in Binary:", bin(num)[2:])
print("Result of Converting", num, "to Binary with QC:", results)
print("Confirm Circuit Gives Correst Result:", list(results.keys())[0]==bin(num)[2:])
# Remove the measurements before performing the quantum Fourier transform
# Do the quantum fourier transform and then return the circuit
qc.remove_final_measurements()
qft(qc, n)
return qc## x = 5
qc = qft_on_number(5)
statevector = Statevector(qc)
plot_bloch_multivector(statevector) ┌───┐ ┌─┐
q46_0: ┤ X ├───┤M├───
└───┘┌─┐└╥┘
q46_1: ─────┤M├─╫────
┌───┐└╥┘ ║ ┌─┐
q46_2: ┤ X ├─╫──╫─┤M├
└───┘ ║ ║ └╥┘
c45: 3/══════╩══╩══╩═
1 0 2
5 in Binary: 101
Result of Converting 5 to Binary with QC: {'101': 1024}
Confirm Circuit Gives Correst Result: True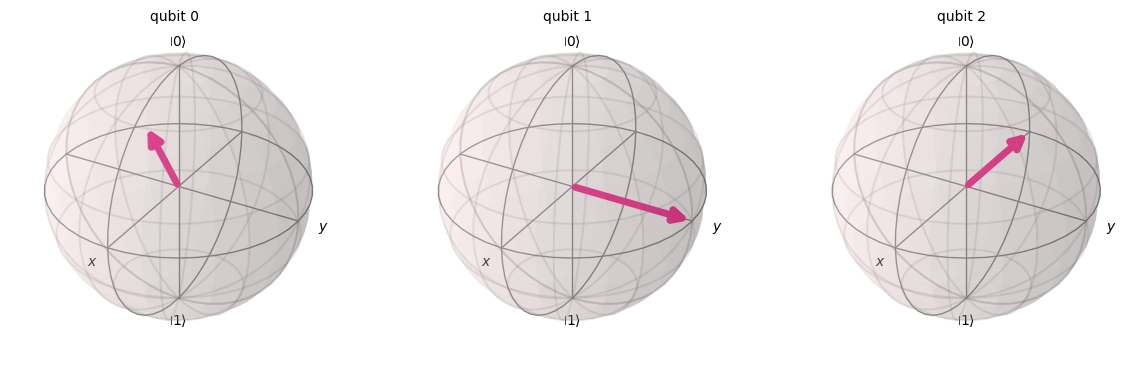
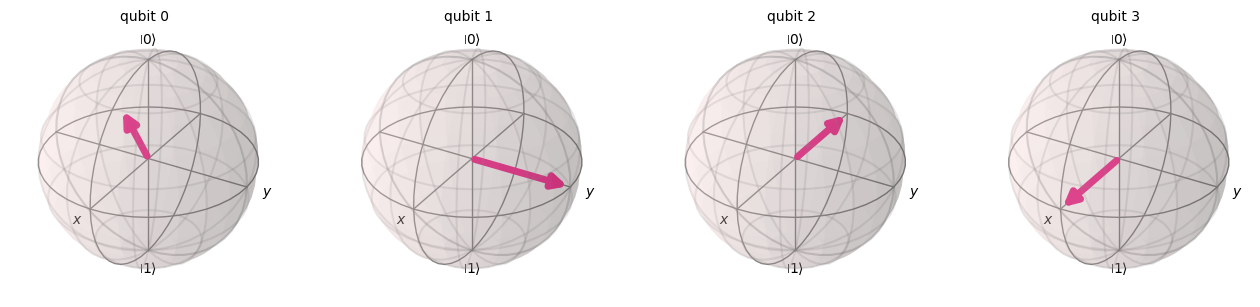
## x = 10
qc = qft_on_number(10)
statevector = Statevector(qc)
plot_bloch_multivector(statevector) ┌─┐
q47_0: ─────┤M├─────────
┌───┐└╥┘ ┌─┐
q47_1: ┤ X ├─╫────┤M├───
└───┘ ║ ┌─┐└╥┘
q47_2: ──────╫─┤M├─╫────
┌───┐ ║ └╥┘ ║ ┌─┐
q47_3: ┤ X ├─╫──╫──╫─┤M├
└───┘ ║ ║ ║ └╥┘
c46: 4/══════╩══╩══╩══╩═
0 2 1 3
10 in Binary: 1010
Result of Converting 10 to Binary with QC: {'1010': 1024}
Confirm Circuit Gives Correst Result: True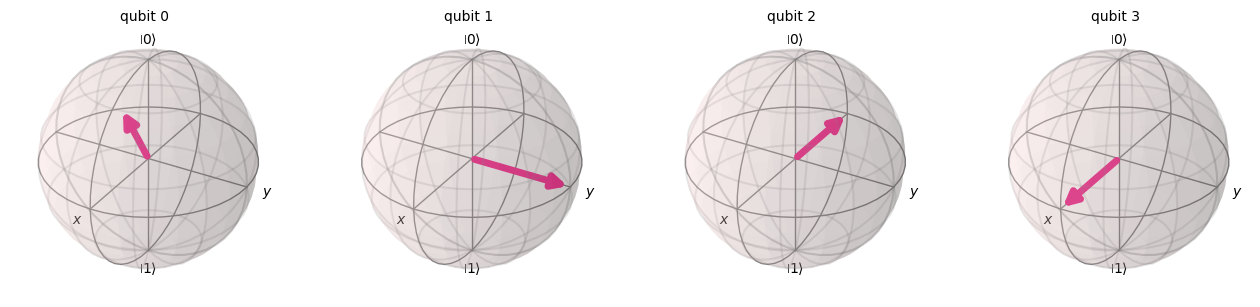
## x = 21
qc = qft_on_number(21)
statevector = Statevector(qc)
plot_bloch_multivector(statevector) ┌───┐ ┌─┐
q48_0: ┤ X ├──────┤M├──────
└───┘┌─┐ └╥┘
q48_1: ─────┤M├────╫───────
┌───┐└╥┘ ║ ┌─┐
q48_2: ┤ X ├─╫─────╫─┤M├───
└───┘ ║ ┌─┐ ║ └╥┘
q48_3: ──────╫─┤M├─╫──╫────
┌───┐ ║ └╥┘ ║ ║ ┌─┐
q48_4: ┤ X ├─╫──╫──╫──╫─┤M├
└───┘ ║ ║ ║ ║ └╥┘
c47: 5/══════╩══╩══╩══╩══╩═
1 3 0 2 4
21 in Binary: 10101
Result of Converting 21 to Binary with QC: {'10101': 1024}
Confirm Circuit Gives Correst Result: True
## x = 35
qc = qft_on_number(35)
statevector = Statevector(qc)
plot_bloch_multivector(statevector) ┌───┐ ┌─┐
q49_0: ┤ X ├─────────┤M├──────
├───┤ └╥┘┌─┐
q49_1: ┤ X ├──────────╫─┤M├───
└───┘┌─┐ ║ └╥┘
q49_2: ─────┤M├───────╫──╫────
└╥┘┌─┐ ║ ║
q49_3: ──────╫─┤M├────╫──╫────
║ └╥┘┌─┐ ║ ║
q49_4: ──────╫──╫─┤M├─╫──╫────
┌───┐ ║ ║ └╥┘ ║ ║ ┌─┐
q49_5: ┤ X ├─╫──╫──╫──╫──╫─┤M├
└───┘ ║ ║ ║ ║ ║ └╥┘
c48: 6/══════╩══╩══╩══╩══╩══╩═
2 3 4 0 1 5
35 in Binary: 100011
Result of Converting 35 to Binary with QC: {'100011': 1024}
Confirm Circuit Gives Correst Result: True
## x = 2
qc = qft_on_number(2)
statevector = Statevector(qc)
plot_bloch_multivector(statevector) ┌─┐
q50_0: ─────┤M├───
┌───┐└╥┘┌─┐
q50_1: ┤ X ├─╫─┤M├
└───┘ ║ └╥┘
c49: 2/══════╩══╩═
0 1
2 in Binary: 10
Result of Converting 2 to Binary with QC: {'10': 1024}
Confirm Circuit Gives Correst Result: True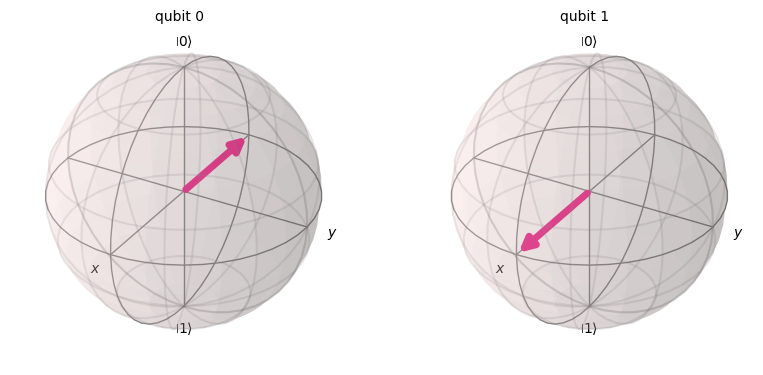
Problem 3
Without using the quantum Fourier transform algorithm we created in class (i.e. without using the recursive formalism), create a quantum circuit that will perform a quantum Fourier transform algorithm on a four-qubit state. Compare the results to relevant examples in Problem #2.
# Create a function that implements the quantum fourier transform algorithm on a four
# qubit system without using recursion
def qft_4_qubit (circuit):
# First apply a Hadamard gate to the highest indexed qubit (3)
circuit.h(3)
# Then add relative phase gates to the target (index 3 qubit) from each
# of the other qubits
circuit.cp(pi/2**(3-0), 0, 3)
circuit.cp(pi/2**(3-1), 1, 3)
circuit.cp(pi/2**(3-2), 2, 3)
# Now apply a Hadamard gate to the index 2 qubit
circuit.h(2)
# And relative phase gates from the index 2 qubit to the index 0 and 1 qubits
circuit.cp(pi/2**(2-0), 0, 2)
circuit.cp(pi/2**(2-1), 1, 2)
# Now a Hadamard gate on the index 1 qubit
circuit.h(1)
# There is only one controlled phase gate now
circuit.cp(pi/2**(1-0), 0, 1)
# Finally, a Hadamard gate to the index 0 (lowest indexed) qubit)
circuit.h(0)
# Swap the order of the qubits before returning the circuit
circuit.swap(0,3)
circuit.swap(1,2)
return circuit# In problem 2, x = 10 has a four digit binary representation, so let's test that
# First set up the quantum circuit which creates 10, this uses the same logic from
# Problem 2
num = 10
n = len(bin(num))-2
bin_rep = bin(num)[2:]
q = QuantumRegister(n)
c = ClassicalRegister(n)
qc = QuantumCircuit(q,c)
for i, bit in enumerate(reversed(bin_rep)):
# If the current bit is a one, then add a not gate to that qubit
if bit == '1':
# i is the control qubit, n is the target qubit
qc.x(i)
# Apply our new QFT function to this circuit and display the results as a Bloch representatiobn
qc = qft_4_qubit(qc)
statevector = Statevector(qc)
plot_bloch_multivector(statevector)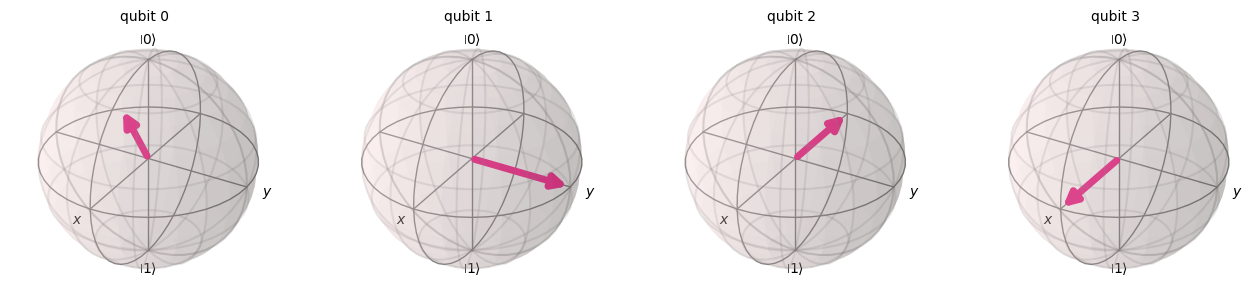
# Compare to the results from Problem 2 which uses the recursive formula
# They are the same!
qc = qft_on_number(10)
statevector = Statevector(qc)
plot_bloch_multivector(statevector) ┌─┐
q45_0: ─────┤M├─────────
┌───┐└╥┘ ┌─┐
q45_1: ┤ X ├─╫────┤M├───
└───┘ ║ ┌─┐└╥┘
q45_2: ──────╫─┤M├─╫────
┌───┐ ║ └╥┘ ║ ┌─┐
q45_3: ┤ X ├─╫──╫──╫─┤M├
└───┘ ║ ║ ║ └╥┘
c44: 4/══════╩══╩══╩══╩═
0 2 1 3
10 in Binary: 1010
Result of Converting 10 to Binary with QC: {'1010': 1024}
Confirm Circuit Gives Correst Result: True