What are quantum computers and how do they compare to classical computers?
Author: Julie Butler
Date Created: June 11, 2024
Last Modified: June 12, 2024
How Does a Classical Computer Work?
A modern classical computer is made up of many different components: RAM, a hard drive (either an HDD or an SSD), a graphics card (which contains a graphical processing unit (GPU)), a monitor, a keyboard, a mouse, and many other components. However, the most important part of the computer is the central processing unit (CPU). This is the part of the computer which controls how all of the other components behave, processes the input to the computer, and determines the output. A CPU is made up of millions or billions of incredibly tiny electrical components called transistors. A transistor is an electrical component which can be in one of two states: it can have electricity flowing through it (the on state) or have no electricity flowing through it (the off state). It is able to switch between these two states depending in the signals it receives. The state of the transistors on the CPU are actually what controls the computer.
Classical Bits
These transistors are the building blocks of classical computers, they are the components which make up the 0’s and 1’s of binary code which tell the computer how to behave. Since the transistors can have two states, we can denote a 0 as no electricity flowing through a transistor and a 1 as electricity flowing through a transistor. Since a computer CPU is made up of millions or billions of transistors then there are millions or billions of digits that can go into constructing the binary code to control a computer. Each of the transistors, or each of the digits going into the computer’s binary code is called a bit, a binary digit. After a human writes computer code (in human language) or input a command to the computer via a mouse or keyboard, the computer’s compilers convert the input into binary code (the computer’s language) that the computer can then process by changing the state of its transistors in the CPU.
Classical Physics
Classical physics is the study of classical mechanics (how things move), electricity, magnetism, optics, and other topics. Classical physics is covered (at least in its basics) in PHY 101 and PHY 102. The important aspect of all of the fields in classical physics is that they are deterministic: given a complete set of initial conditions and knowing everything about the system, you can predict the state the system will be in at any given time. This may be complicated but, at least theoretically, it is possible.
Quantum Physics (Quantum Mechanics)
While classical physics applies to most things we see and interact with in everyday life, it breaks down at the microscopic scale. Molecules, atoms, nuclei, electrons, protons, and other very small particles obey a different type of physics called quantum physics or quantum mechanics. At this scale, the physics we know breaks down and we are left with a very different set of rules. At this scale, instead of describing an object using things like its position, velocity, and momentum, we instead use something called a wavefunction. A wavefunction is not something that is physically real, but rather it is a mathematical representation of the object we are trying to model. By performing mathematical operations on the wavefunction, we are able to determine the physical quantities of the object. However, there is a caveat to using quantum physics to determine the properties of an object; quantum mechanics is a probabilistic system, meaning that we can never know the physical properties of a system for certain. Instead, we can calculate the most likely result of a measurement.
Important Concepts in Quantum Mechanics
Particle-Wave Duality
Surprisingly, when things get very small, they do not behave entirely as matter. Very small objects do have some properties associated with matter, therefore we call them particles, but they also have some properties associated with waves. Experiments have been done which show that electrons, protons, and neutrons display the same behavior of light waves. Therefore, we say that these quantum mechanical systems have properties of both particles and waves, or that they have a particle-wave duality. This duality is the reason we call the mathematical representation of a quantum mechanical system a wavefunction. Because of the wave-like nature of particles, they also obey all properties of waves, such as superposition and interference, discussed below.
Superposition
A classical object, like a ball, have many different states. For example, a ball can be on the ground, be picked up by a person, or be tossed in the air. These all describe different states the ball can have and in each of the state different rules govern it motion. However, the ball can only be in one of these states at a time. A ball cannot be simultaneously tossed through the air and be sitting on the ground. The same cannot be said about particles, however. One of the strange things about quantum mechanics, is that mathematically we say that a particle can have many different states and can be in one or more of them at the same time. Let’s assume, that like the ball, a particle can be in three different state. Let’s denote these state as \(\psi_1\), \(\psi_2\), and \(\psi_3\). The particle can be in just \(\psi_1\), \(\psi_2\), or \(\psi_3\), or it can be in a combination of two or more of the states such as \(\psi_1\) + \(\psi_3\) or \(\psi_1\)+\(\psi_2\)+\(\psi_3\).
The famous thought experiment used to explain this phenomena is Schrodinger’s cat, proposed by Erwin Schrodinger. The thought experiment goes as follows. A cat is placed into a box and the lid is shut. Inside the box is a vial of poison which is set to break at some unknown point. When it breaks, it will kill the cat, but there is no way to know if the vial has broken unless the box is opened. Therefore, while the box is closed the cat can be thought of as in a superposition of both alive and dead. These are the two states it can be in and there is no way to know which one it is in, so we just say it is in both.
Measurement and Collapse
When you measure a particle to determine some property of it, you force the wavefunction of the particle to collapse into a single state. Phrased another way, though we think of a particle in being in a superposition of many states, when you measure it, you will only get the result of a single state. When you open the box containing the cat, you determine rather it is alive or dead; it is no longer in a superposition of both states.
Entanglement
If two particles come near each other, then it is possible for them to become “entangled”. This entanglement is much as it seems, the particles’ wavefunctions become intertwined and cannot be separated. The particles then do not behave independently but as a dependent system; changing the state of one of the particles changes the state of the other particle. More than two particles can become entangled as well, creating entire systems where a slight change to one particle can change the state of every other particle. Note that entanglement is not necessarily permanent, particles can untangle in the correct circumstances (high temperature for example). The process of a system un-entangling itself is called decoherence.
Qubits
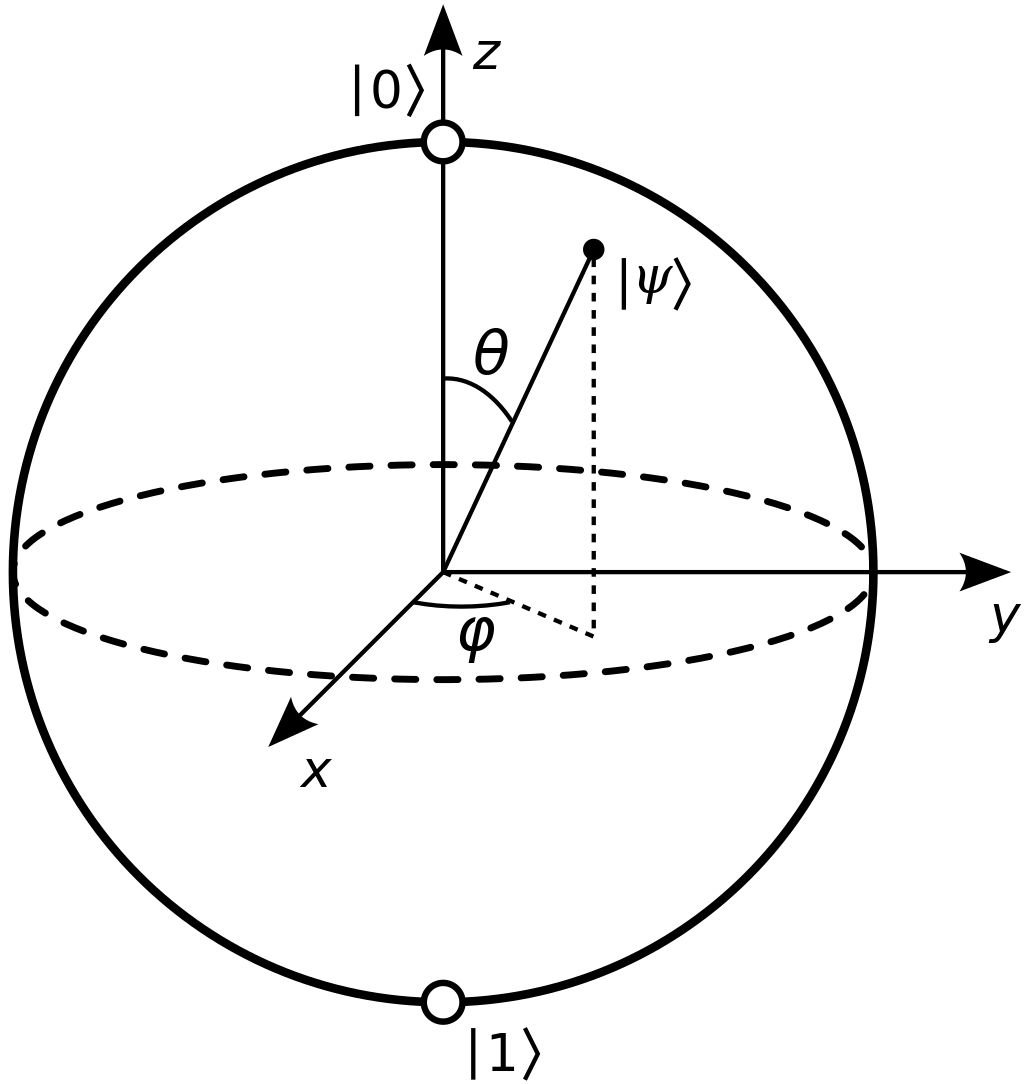
Just like bits are the building blocks of a classical computer, the building blocks of a quantum computer are called qubits (a mash-up of “quantum” and “bit”). Like a classical bit, a qubit can be represented as either a 0 or a 1, but unlike a classical bit, a qubit can also be represented by any number between 0 and 1 as well (a superposition of 0 and 1). The Bloch sphere is typically used to visualize and think about qubit behavior (though note this is not a physical representation of how qubits switch states). You can think of a qubit as an arrow in a sphere, where the arrow can swing around. If the arrow is straight up then it is in the 0 state and if the arrow is straight down it is in the 1 state. If the arrow is in any other orientation, then it is in a superposition of the 0 and 1 states. When we measure a qubit, we collapse its wavefunction to either a 0 or a 1 (not both), with different probabilities of the qubit ending up in each state; quantum computing is probabilistic, not deterministic like classical computing. If we think about measuring the qubit depicted in the diagram above, since the qubit is pointing slightly down, there is a greater probability that the qubit will end up in the 1 state when measured than the 0 state, but it is still possible to obtain a 0 measurement since the qubit is not totally in the 1 state. Everything we write a program for a quantum computer, we have to consider the likelihood we will get the result we want from a measurement and how we can tune the quantum computer towards giving us the desired result most of the time.
What is a Quantum Computer?

A quantum computer is a collection on qubits and gates, which are used to control the state of the qubits without measuring (and this collapsing) them. All of the qubits of a quantum computer are entangled so that they can work together. Additionally, a quantum computer also includes a large amount of wiring (both input and output) and cooling (a quantum computer needs to run at supercool temperatures, near absolute zero). In fact, in photos of quantum computers, only the very bottom of the apparatus contains the qubits, the rest of the device is used for support.
You “write” quantum computing code, or control the output of a quantum computer, by applying quantum logic gates to certain qubits in a certain order. After all of the gates are applied, you measure the state of all the qubits, collapsing the superposition, and determining the answer of the calculation. While we will get into the exact functions of the quantum gates in a few lectures, you can think of quantum gates as rotating the qubit around the Bloch sphere, making the result of measuring the qubit to tend towards one result or the other. This part will make more sense in the next few weeks as we expand on everything covered today in more detail.
There are many ways to make a quantum computer, and by this I mean there are many ways to create a qubit. We will discuss the details of implementing a quantum computer near the end of this course, but each method of creating a quantum computer uses a quantum mechanical system (usually a particles but sometimes light) to represent a qubit. This system needs to have to states (one to represent a 0 and the other to represent a 1) and the system has to be able to switch between these to states.
Are Quantum Computers Better than Classical Computers?
The short, the not very satisfying answer is…maybe. There are many problems that a quantum computer struggles with that can be very easily solved on a classical computer. However, at the same time, there are specific problems which are complex to solve on a classical computer that can be solved on a quantum computer much faster. This has to do with the differences between bits and qubits; a bit can only be at one state at a time but qubits can be in a superposition of many states at the same time. This superposition can be exploited to solve some types of problems incredibly quickly. If this does not make sense right now, don’t worry! It should make sense over the next few weeks as we start to dive deeper into what this means.
While there are some algorithms that perform better on quantum computers than classical computers (we will explore many of these in this course) the scalability of quantum computers current limits the real applications. The scalability of a computer refers how easy is it to “upgrade” the computer to a have more computational power. With a classical computer, it can be scaled up by increasing the number of transistors on the CPU (increasing the clockspeed of the CPU). This increases the number of bits available to perform calculations. While this is not hard for a classical computer (we are actually really good at this in the modern day), increasing the number of qubits on a quantum computer is quite complicated. Most quantum computers available today have about 130 qubits. While this is not a lot, it is enough to do some pretty cool calculations! Scaling a quantum computer up significantly will be a large technological and engineering challenge, mostly related to the extreme cooling that is required (quantum computers only work at extremely low temperatures, near absolute zero).
Shor’s Algorithm
One of the most famous quantum algorithms is Shor’s algorithm. Multiplying two numbers together, no matter how large they are, is not a complicated task for classical computers. However, prime factorization (finding two prime numbers which can be multiplied together to get the desired result) is difficult on classical computers, especially for large numbers. The reason is that there are many numbers smaller than a given number to factor, and each of them needs to be considered as a factor until proven otherwise. Put another way, the search space to find the factors of number is large. Some modern encryption schemes make use of the fact that finding the prime factors of a very large number is basically impossible. In these encryption schemes, using in banks among other applications, one side of the authentication has two very large prime numbers, which when multiplied togehter, results in the number stored on the other side of the encryption scheme. Unless you can find the exact two large prime numbers which are needed, you cannot break the encryption.
Computational complexity refers to the time and resources needed by an algorithm as the size of the problem increases. Factorization has a rather high computational complexity; to factory an N digit number using classical algorithms, the time and resource requirements grow by \(2^{N/2}\). This is referred to exponential scaling, since the time needed grows exponentially each time another digit is added. Factoring a 2 digit number will take twice as long as a 1 digit number, a 4 digit number takes four times as long as a 1 digit number, factoring a 8 digit number takes sixteen times as long as a 1 digit number, and so on. This means that it is nearly impossible (both with time and resource limitations) to factor many digit numbers.
Thirty years ago, the mathematician Peter Shor proposed an algorithm to quickly factor large numbers, but it had to run on a quantum computer instead of a classical computer. Shor’s algorithm is able to find the prime factors of a number significantly faster than the classical algorithms, with a computational complexity of only log(N) for an N digit number. This means that factoring a 2 digit number is only 30% longer than a 1 digit number, factoring a 4 digit number is only 60% slower than a 1 digit number. Shor’s algorithm has polynomial scaling, which is significantly better than the exponential scaling of the classical algorithm.
Shor’s algorithm could pose a major hazard to modern encryption schemes, but, luckily for us as bank users but unluckily for us as quantum computer users, current quantum computers are too small to handle large factorization problems. This is one of the current problems with quantum computers discussed above, they are quite small currently and scalability is a hard problem to overcome. Quantum scientists are simultaneously working on increasing the size of quantum computers (meaning Shor’s algorithm could be applied to larger numbers) but also on quantum encryption algorithms, which would replace the current prime factor encryption and will be harder to crack on a classical or quantum computer.
Grover’s Search Algorithm
Search algorithms are very common in the field of computer science and various levels of efficiency. Searching an ordered list of data can be quite fast, but the same cannot be said for unordered data. The very best classical algorithm can search an N-element unordered list with computational complexity N. This means that it takes twice as long to search a four-element list as a two-element list, four times as long to search an eight-element list as a two-element list, and so on.
Grover’s search algorthm is a quantum searching algorithm for unordered data. It has a computational complexity of \(\sqrt{N}\), which gives it quadratic speed-up over classical algorithms. While the main goal of quantum algorithm engineers is to create algorithms which have an exponential speed-up compared to classical algorithms, a quadratic speed-up is still very good, especially with the length of the list grows large.
There are some limitations to Grover’s algorithm. Like Shor’s algorithm, current implementations are limited by the size of the quantum computers. Additionally, the process of getting data to a quantum computer can be a difficult process and currently being improved. We will discuss both of these limitations in more detail if a few weeks when we cover Grover’s algorithm in more detail.
What Else Can You Use a Quantum Computer For?
One of the most exciting potential applications of quantum computing is the simulation of quantum systems. Simulating quantum systems is of importance across many fields of chemistry and physics, but simulating as few as 30 particles can be quite difficult with classical computing. Richard Fenyman, a famous physicist, made the (seemingly obvious) suggestion that quantum simulations would run better on a classical computer than a quantum computer since using a quantum computer would been simulating a quantum system with a quantum system. Though modern quantum computers are still quite small, there are already exciting results from quantum simulations of various systems on these computers.
The second application of quantum computers is in optimization problems. Quantum optimization algorithms have the promise to solve optimizations that cannot be solved on a classical computer and to drastically speed up classical optimization problems. Once these optimization algorithms are realized on the large scale, they have the ability to impact almost every field, including machine learning, the natural sciences, business, finance, and many more.
Third, quantum computers have the ability to speed up machine learning problems, a field called quantum machine learning. This is due in part to the beetter optimization discussed above and also how quantum computers can handle linear algebra calculations. Some simple machine learning algorithms have already shown speed-up on a quantum computer, such as k-nearest neighbors, and a lot of research is currently going into perfecting quantum neural networks, a quantum computing implementation of neural networks.
The next two fields which will benefit from quantum computing are financial modeling and climate change and weather forecasting. These are classically complex modeling tasks because the model can be influence by so many internal and external factors. Inf act, modeling the weather can be considered a chaotic system, since minor changes can have large effects over a long time.
Finally, as we discussed in the Shor’s algorithm section, the rise of quantum computer could be a major cybersecurity and encryption concern. However, one of the applications of quantum computer is quantum cryptography and quantum key distribution. These fields are working to re-do modern encryption schemes using quantum technology that will be harder to break.