# Needed to set up the quantum circuit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
# Needed to simulate running a quantum computer
from qiskit_aer import AerSimulator
# Neded to visualize the results of running a quantum computer
from qiskit.visualization import plot_histogramQuantum Measurement, Wavefunction Collapse, and Entanglement on a Quantum Computer
Author: Julie Butler
Date Created: September 4, 2024
Last Modified: September 5, 2024
Simulating Two Qubits
# Map two qubits to two classical bits
q = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q, c)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw()) ┌─┐
q18_0: ┤M├───
└╥┘┌─┐
q18_1: ─╫─┤M├
║ └╥┘
c17: 2/═╩══╩═
0 1 Applying the Controlled NOT (CNOT) Gate
# Map two qubits to two classical bits
q = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q, c)
# Add a CX (CNOT) gate on control qubit 0 and target qubit 1
qc.cx(0, 1)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌─┐
q19_0: ──■──┤M├───
┌─┴─┐└╥┘┌─┐
q19_1: ┤ X ├─╫─┤M├
└───┘ ║ └╥┘
c18: 2/══════╩══╩═
0 1 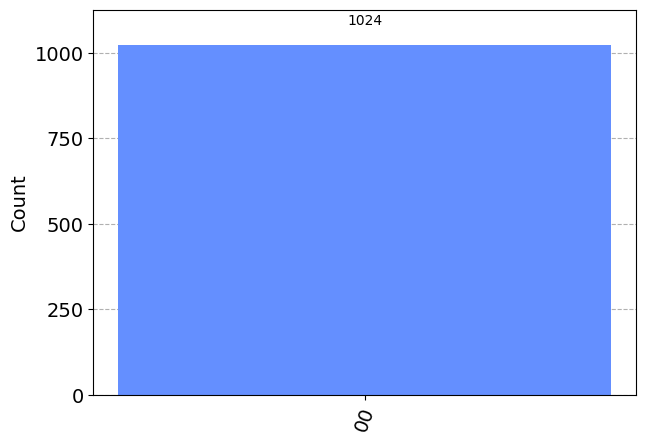
Let’s try switching the control and target qubits.
# Map two qubits to two classical bits
q = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q, c)
# Add a CX (CNOT) gate on control qubit 0 and target qubit 1
qc.cx(1, 0)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌───┐┌─┐
q20_0: ┤ X ├┤M├───
└─┬─┘└╥┘┌─┐
q20_1: ──■───╫─┤M├
║ └╥┘
c19: 2/══════╩══╩═
0 1 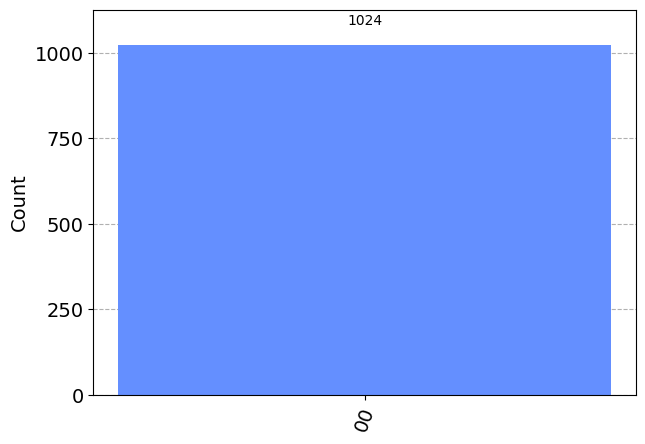
Finally, try switching the control qubit from a \(|\uparrow\rangle\) (0) state to a \(|\downarrow\rangle\) (1) state to see how this changes things. We will change the control qubit using a one qubit NOT gate.
# Map two qubits to two classical bits
q = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q, c)
# Apply a NOT gate to the control qubit
qc.x(0)
# Add a CX (CNOT) gate on control qubit 0 and target qubit 1
qc.cx(0, 1)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌───┐ ┌─┐
q21_0: ┤ X ├──■──┤M├───
└───┘┌─┴─┐└╥┘┌─┐
q21_1: ─────┤ X ├─╫─┤M├
└───┘ ║ └╥┘
c20: 2/═══════════╩══╩═
0 1 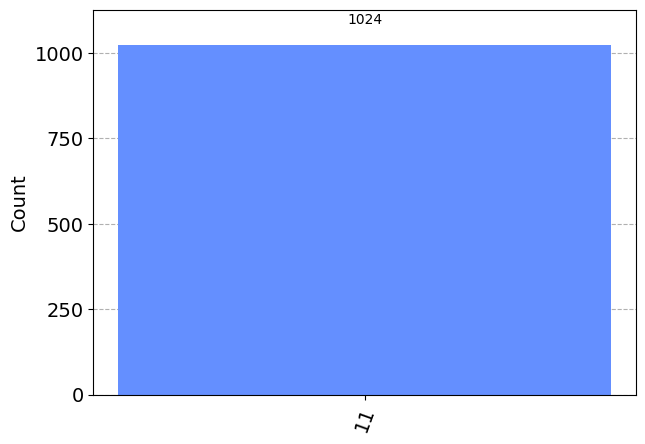
Two Qubit SWAP Gate
First let’s look at just a two qubit state with a NOT gate applied to the first qubit.
# Map two qubits to two classical bits
q = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q, c)
# Apply a NOT gate to the control qubit
qc.x(0)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌───┐┌─┐
q23_0: ┤ X ├┤M├
└┬─┬┘└╥┘
q23_1: ─┤M├──╫─
└╥┘ ║
c22: 2/══╩═══╩═
1 0 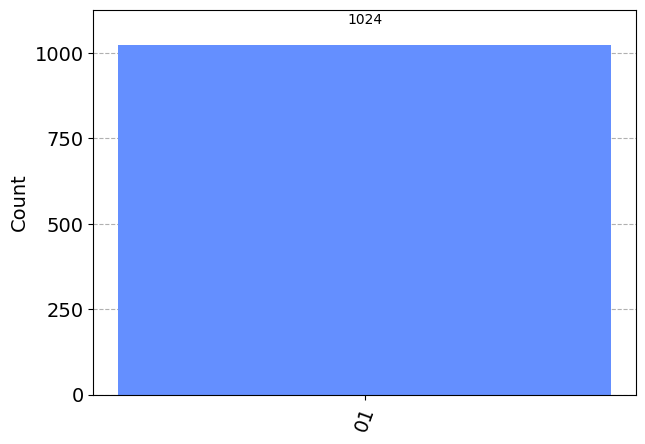
Now let’s add a SWAP gate after the NOT gate and see if we can change the order of the qubits.
# Map two qubits to two classical bits
q = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q, c)
# Apply a NOT gate to the control qubit
qc.x(0)
# Add a SWAP gate on qubit 0 and qubit 1
qc.swap(0, 1)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌───┐ ┌─┐
q22_0: ┤ X ├─X─┤M├───
└───┘ │ └╥┘┌─┐
q22_1: ──────X──╫─┤M├
║ └╥┘
c21: 2/═════════╩══╩═
0 1 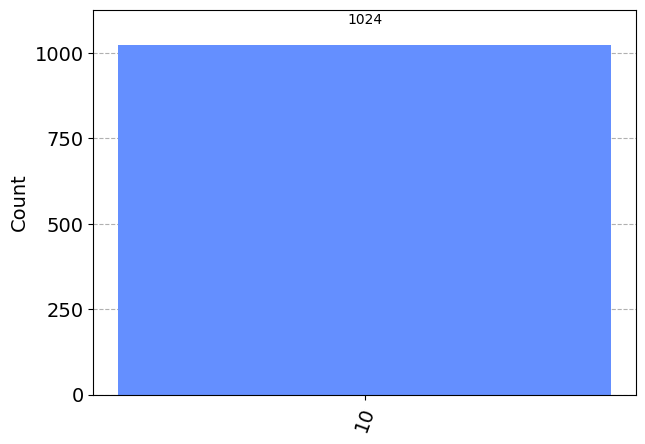
Create the First Bell State
The below code creates the \(|\Phi^+\rangle\) Bell state. How could you adjust this to create other Bell states?
# Map two qubits to two classical bits
q = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q, c)
# Add a H gate on qubit 0
qc.h(0)
# Add a CX (CNOT) gate on control qubit 0 and target qubit 1
qc.cx(0, 1)
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌───┐ ┌─┐
q17_0: ┤ H ├──■──┤M├───
└───┘┌─┴─┐└╥┘┌─┐
q17_1: ─────┤ X ├─╫─┤M├
└───┘ ║ └╥┘
c16: 2/═══════════╩══╩═
0 1 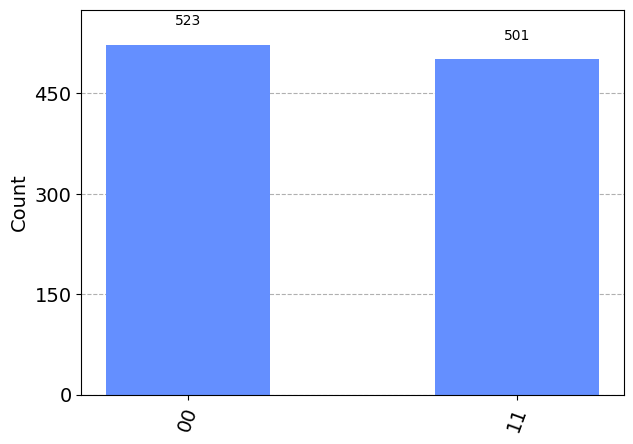
Creating a Three Qubit State
# Map two qubits to two classical bits
q = QuantumRegister(3)
c = ClassicalRegister(3)
qc = QuantumCircuit(q, c)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw()) ┌─┐
q24_0: ┤M├──────
└╥┘┌─┐
q24_1: ─╫─┤M├───
║ └╥┘┌─┐
q24_2: ─╫──╫─┤M├
║ ║ └╥┘
c23: 3/═╩══╩══╩═
0 1 2 Quantum Gates With Three Qubits: Some Examples
# THREE QUBIT EXAMPLE
# Map two qubits to two classical bits
q = QuantumRegister(3)
c = ClassicalRegister(3)
qc = QuantumCircuit(q, c)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌─┐
q25_0: ┤M├──────
└╥┘┌─┐
q25_1: ─╫─┤M├───
║ └╥┘┌─┐
q25_2: ─╫──╫─┤M├
║ ║ └╥┘
c24: 3/═╩══╩══╩═
0 1 2 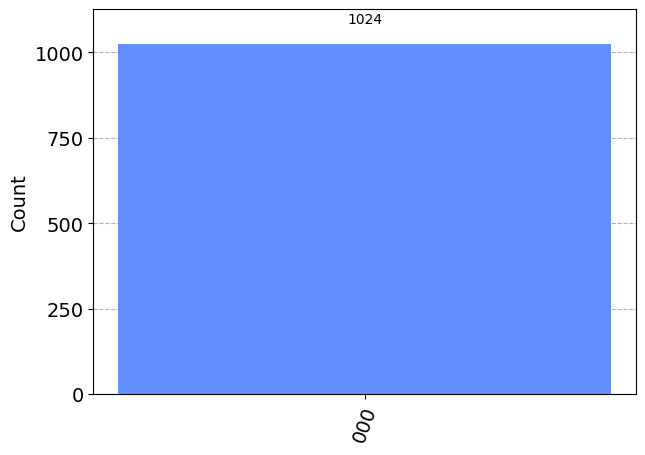
## FREDKIN or CSWAP EXAMPLE
# Map two qubits to two classical bits
q = QuantumRegister(3)
c = ClassicalRegister(3)
qc = QuantumCircuit(q, c)
# Apply a Hadamard gate to the first qubit, which will be our control
qc.h(0)
# Apply a not gate to the second qubit, which is one of the targets
qc.x(1)
qc.cswap(0,1,2)
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌───┐ ┌─┐
q31_0: ┤ H ├─■─┤M├──────
├───┤ │ └╥┘┌─┐
q31_1: ┤ X ├─X──╫─┤M├───
└───┘ │ ║ └╥┘┌─┐
q31_2: ──────X──╫──╫─┤M├
║ ║ └╥┘
c30: 3/═════════╩══╩══╩═
0 1 2 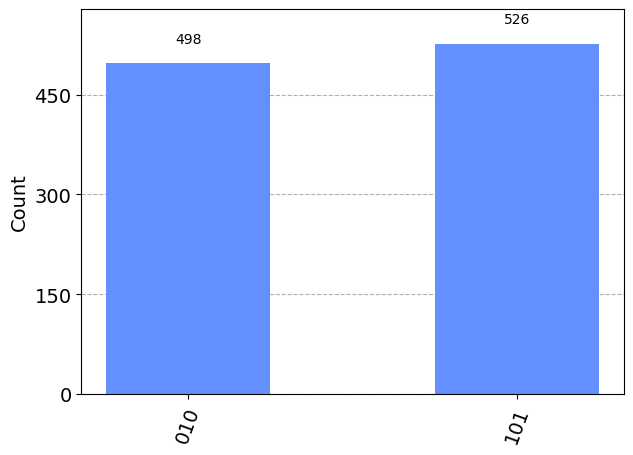
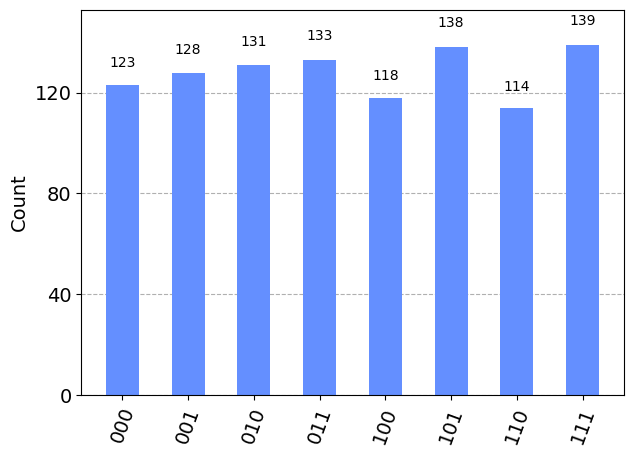
# THREE HADAMARD GATES EXAMPLE
# Map two qubits to two classical bits
q = QuantumRegister(3)
c = ClassicalRegister(3)
qc = QuantumCircuit(q, c)
# Apply a Hadamard gate individually to each qubit
qc.h(0)
qc.h(1)
qc.h(2)
# Measure the circuit and print the circuit diagram
qc.measure(q, c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results) ┌───┐┌─┐
q32_0: ┤ H ├┤M├──────
├───┤└╥┘┌─┐
q32_1: ┤ H ├─╫─┤M├───
├───┤ ║ └╥┘┌─┐
q32_2: ┤ H ├─╫──╫─┤M├
└───┘ ║ ║ └╥┘
c31: 3/══════╩══╩══╩═
0 1 2