Lecture 9 Example Solutions

Note that the below solutions are only examples, there are many possible solutions to each challenge.

For each of the below challenge questions:

Draw (by hand) the predicted quantum circuit that is needed to achieve the desired results
Use qiskit to build the quantum circuit and ensure that qiskit circuit matches your predicted circuit
Use Aer to simulate the circuit and ensure you get the desired results. Remember that when mapping from qubits to classical bits \(|\uparrow\rangle\) = 0 and \(|\downarrow\rangle\) = 1.

# Needed to set up the quantum circuit
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
# Needed to simulate running a quantum computer
from qiskit_aer import AerSimulator
# Neded to visualize the results of running a quantum computer
from qiskit.visualization import plot_histogram

Challenge 1

Create a circuit that creates the state \(|\uparrow\uparrow\uparrow\uparrow\rangle\) only and that uses two or more gates.

q = QuantumRegister(4)
c = ClassicalRegister(4)
qc = QuantumCircuit(q,c)
qc.z(0)
qc.z(0)
qc.z(0)
qc.measure(q,c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results)

      ┌───┐┌───┐┌───┐┌─┐
q3_0: ┤ Z ├┤ Z ├┤ Z ├┤M├
      └┬─┬┘└───┘└───┘└╥┘
q3_1: ─┤M├────────────╫─
       └╥┘  ┌─┐       ║ 
q3_2: ──╫───┤M├───────╫─
        ║   └╥┘  ┌─┐  ║ 
q3_3: ──╫────╫───┤M├──╫─
        ║    ║   └╥┘  ║ 
c2: 4/══╩════╩════╩═══╩═
        1    2    3   0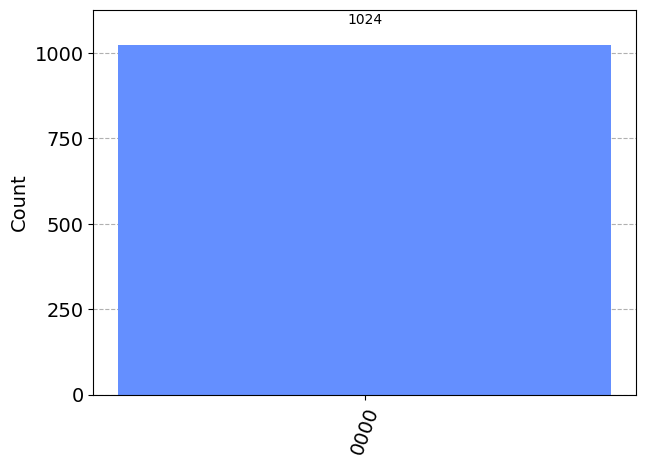

Challenge 2

Create the state \(|\uparrow\downarrow\downarrow\downarrow\uparrow\rangle\) using the Fredkin gate and any number of other gates.

q = QuantumRegister(5)
c = ClassicalRegister(5)
qc = QuantumCircuit(q,c)
qc.x(1)
qc.x(2)
qc.x(3)
qc.cswap(1,2,3)
qc.measure(q,c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results)

           ┌─┐            
q4_0: ─────┤M├────────────
      ┌───┐└╥┘   ┌─┐      
q4_1: ┤ X ├─╫──■─┤M├──────
      ├───┤ ║  │ └╥┘┌─┐   
q4_2: ┤ X ├─╫──X──╫─┤M├───
      ├───┤ ║  │  ║ └╥┘┌─┐
q4_3: ┤ X ├─╫──X──╫──╫─┤M├
      └┬─┬┘ ║     ║  ║ └╥┘
q4_4: ─┤M├──╫─────╫──╫──╫─
       └╥┘  ║     ║  ║  ║ 
c3: 5/══╩═══╩═════╩══╩══╩═
        4   0     1  2  3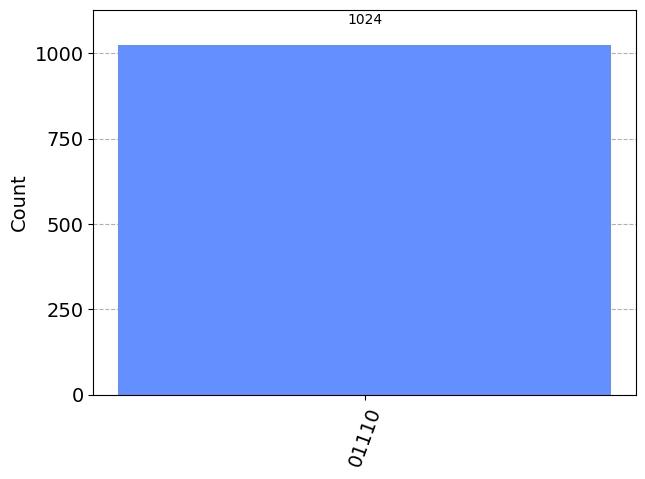

Challenge 3

Create a circuit that produces \(|\downarrow\uparrow\uparrow\downarrow\rangle\) and at least one other state.

q = QuantumRegister(4)
c = ClassicalRegister(4)
qc = QuantumCircuit(q,c)
qc.x(0)
qc.x(3)
qc.h(1)
qc.measure(q,c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results)

      ┌───┐   ┌─┐      
q6_0: ┤ X ├───┤M├──────
      ├───┤   └╥┘┌─┐   
q6_1: ┤ H ├────╫─┤M├───
      └───┘┌─┐ ║ └╥┘   
q6_2: ─────┤M├─╫──╫────
      ┌───┐└╥┘ ║  ║ ┌─┐
q6_3: ┤ X ├─╫──╫──╫─┤M├
      └───┘ ║  ║  ║ └╥┘
c5: 4/══════╩══╩══╩══╩═
            2  0  1  3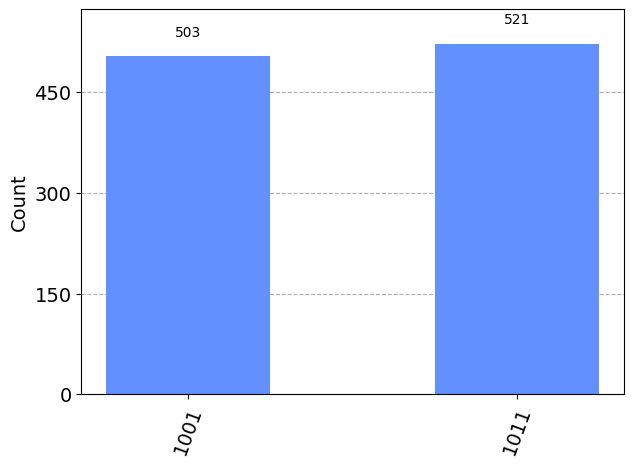

Challenge 4

Create a circuit which has only one possible outcome (\(|\downarrow\uparrow\downarrow\uparrow\downarrow\rangle\)) using at most one single qubit gate and any number of two and three qubit gates.

q = QuantumRegister(5)
c = ClassicalRegister(5)
qc = QuantumCircuit(q,c)
qc.x(0)
qc.cx(0,2)
qc.cx(0,4)
qc.measure(q,c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results)

       ┌───┐             ┌─┐   
q14_0: ┤ X ├──■────■─────┤M├───
       └┬─┬┘  │    │     └╥┘   
q14_1: ─┤M├───┼────┼──────╫────
        └╥┘ ┌─┴─┐  │  ┌─┐ ║    
q14_2: ──╫──┤ X ├──┼──┤M├─╫────
         ║  └┬─┬┘  │  └╥┘ ║    
q14_3: ──╫───┤M├───┼───╫──╫────
         ║   └╥┘ ┌─┴─┐ ║  ║ ┌─┐
q14_4: ──╫────╫──┤ X ├─╫──╫─┤M├
         ║    ║  └───┘ ║  ║ └╥┘
c13: 5/══╩════╩════════╩══╩══╩═
         1    3        2  0  4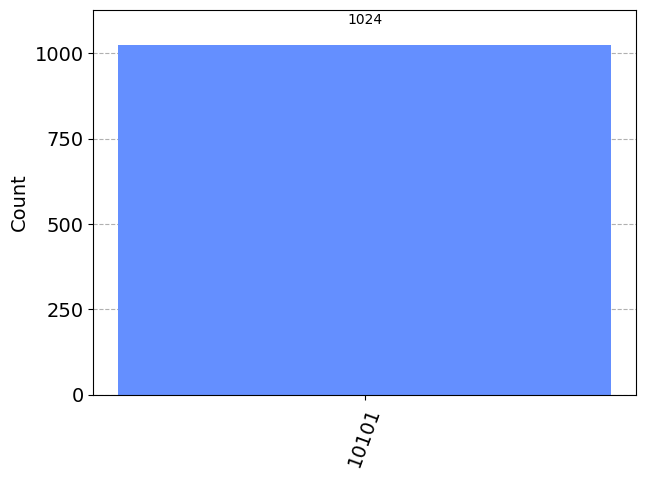

Challenge 5

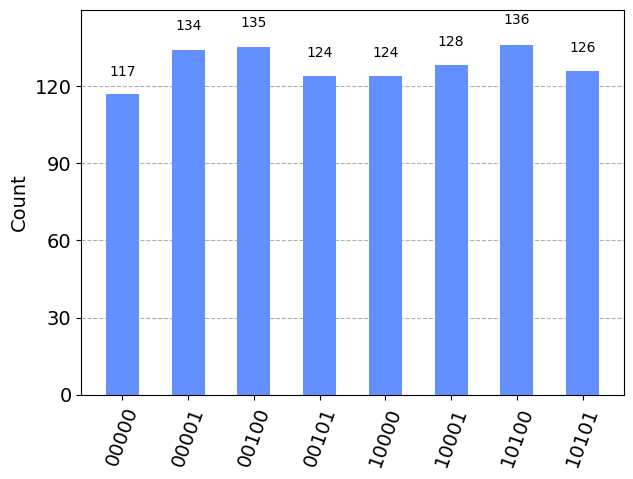
An \(n\) qubit circuit has \(2^n\) possible combinations of qubits (\(2^n\) possible qubits). Create a 5 qubit circuit that has at least 6 possible outcomes. You must use two different types gates in addition to any number of Hadamard gates.

q = QuantumRegister(5)
c = ClassicalRegister(5)
qc = QuantumCircuit(q,c)

qc.h(0)
qc.h(2)
qc.h(4)

qc.measure(q,c)
print(qc.draw())
simulator = AerSimulator()
results = simulator.run(qc).result().get_counts()
plot_histogram(results)

       ┌───┐      ┌─┐      
q48_0: ┤ H ├──────┤M├──────
       └───┘┌─┐   └╥┘      
q48_1: ─────┤M├────╫───────
       ┌───┐└╥┘    ║ ┌─┐   
q48_2: ┤ H ├─╫─────╫─┤M├───
       └───┘ ║ ┌─┐ ║ └╥┘   
q48_3: ──────╫─┤M├─╫──╫────
       ┌───┐ ║ └╥┘ ║  ║ ┌─┐
q48_4: ┤ H ├─╫──╫──╫──╫─┤M├
       └───┘ ║  ║  ║  ║ └╥┘
c47: 5/══════╩══╩══╩══╩══╩═
             1  3  0  2  4