Classification Problems

CSC/DSC 340 Week 4 Slides

Author: Dr. Julie Butler

Date Created: August 13, 2023

Last Modified: August 14, 2023

What are Classification Problems?

• Goal: Determine what “class” a data point belongs to

• Regression: output can be any real number

• Classification: output can only be taken from finite and discrete set

Classification Examples

• Can the condition of a car be determined from its price and odometer reading?

• Can the species of a plant or animal be determined from various measurements?

• Can the sex of an animal be determined from various measurements?

• Can handwritten numbers be converted to text (MNIST Data Set)?

• Can pictures of clothes be identified?

• Can pictures be determined to contain dogs or cats?

Types of Classification Problems

• Binimal Classifier: data is sorted into one of two categories

• Multiclass Classifier: data is sorted into one of three or more categories

• Multilabel Classifier: data can belong to more than one category

Classifiers

• Ridge Classifier (this week)

• Stochastic Gradient Descent (Hands-On Chapter 3)

• Support Vector Machines (not covered)

• Neural Networks/Convolutional Neural Networks (covered later)

Ridge Classifier

• Scikit-Learn implementation

• Using ridge regression but converts it into a classification problem

• Binomial classification

  • Inputs are mapped to outputs between -1 and 1

  • Class 0 corresponds to a negative output and class 1 corresponds to a positive output

• Multiclass classification

  • Treat as multi-output regression problem and output with higest value is the category

• Simple classification algorithm but computationally effecient

Error Metrics

• The error metrics we have mean using are not suitable to determine the performance of a classifier

• New error metrics

  • Accuracy Score

  • Confusion Matrix

  • Other error metrics are covered in Chapter 3 of Hands-On Machine Learning

Accuracy Score

\[ Score = \frac{Number\ of\ Correct\ Predictions}{Total\ Number\ of\ Data\ Points}\]

• A score of 1.0 means 100% of the predictions are classified correctly

• A score of 0.0 means 0% of the predictions are classified correctly

Confusion Matrix

• Each row represents an actual class, each column represents a predicted class

• Numbers of the main diagonal are correct predictions and numbers on the off diagonal elements are in correct predictions Image Source

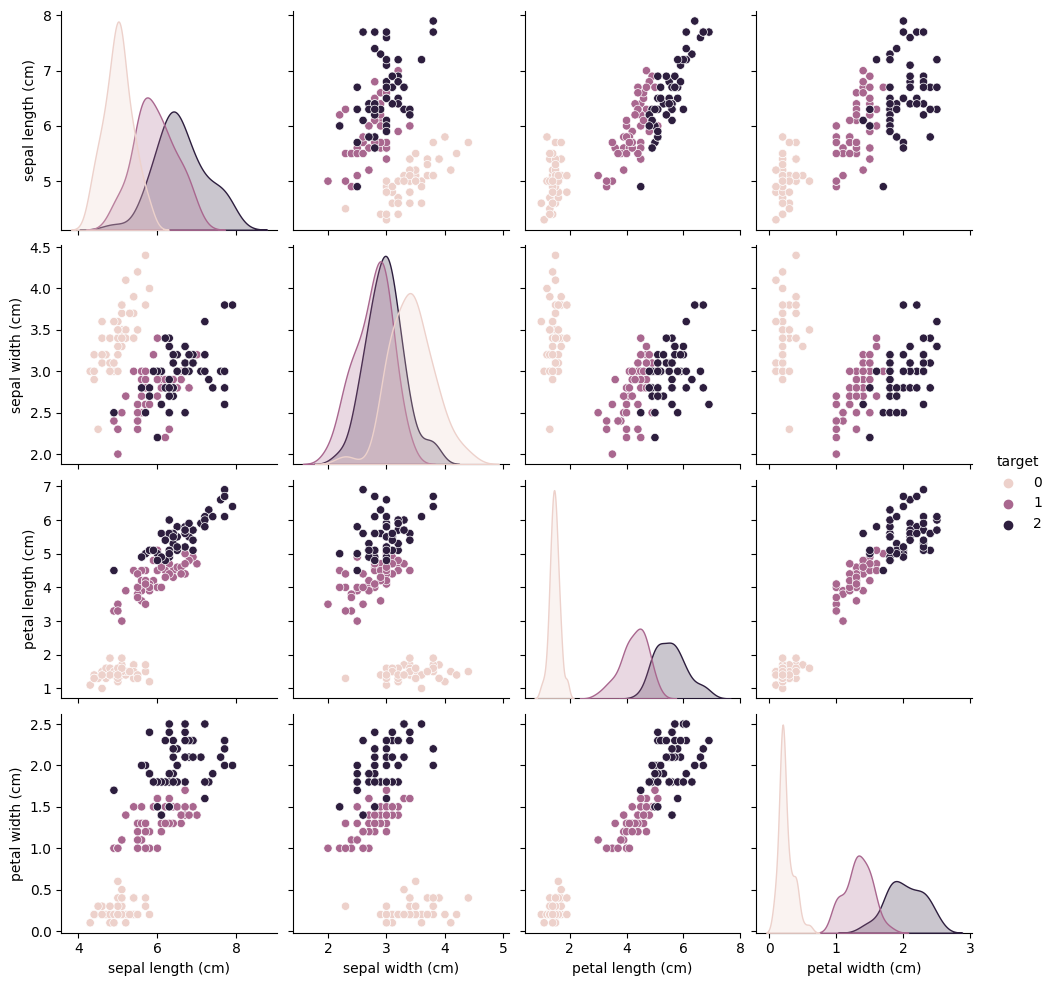
Example: The Iris Data Set and the Ridge Classifier

• The Iris Data Set is a famous classification data set

• Each point contains measurements of different parts of the flower and the specific variety of iris it belongs to

• Goal is to predict what type of iris each flower is

• Image Source

##############################
##          IMPORTS         ##
##############################
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import RidgeClassifier
from sklearn.model_selection import train_test_split

# Load the iris dataset from sklearn
iris = load_iris()

# Convert the iris dataset to a pandas dataframe
iris_data = pd.DataFrame(iris.data, columns=iris.feature_names)

# Add the target variable to the dataframe
iris_data['target'] = iris.target

# Determine what data the iris data set contains
iris_data

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

150 rows × 5 columns

# Create a pairplot with the color of each dot corresponding to the type of iris
sns.pairplot(iris_data, hue='target')

/Users/juliehartley/Library/Python/3.9/lib/python/site-packages/seaborn/axisgrid.py:118: UserWarning: The figure layout has changed to tight
  self._figure.tight_layout(*args, **kwargs)

<seaborn.axisgrid.PairGrid at 0x156cb47c0>

# Features are the inputs/X-data
features = iris_data.drop(columns=['target'])

# labels are the outputs/y-data/targets
labels = iris_data['target']

# Splot the data into training and test data sets
X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size=0.2)

# Define, train, and predict with a ridge classifier
ridge_classifier = RidgeClassifier()
ridge_classifier.fit(X_train, y_train)
y_pred = ridge_classifier.predict(X_test)

# Calculate the accuracy score, where 1.0 means 100% of predictions are correct
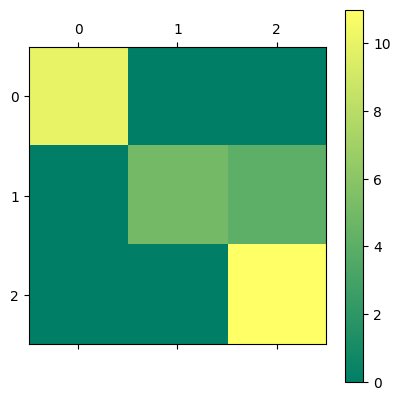
print(ridge_classifier.score(X_test, y_test))

0.8666666666666667

# Print out a confusion matrix
confusion_matrix(y_test, y_pred)

array([[10,  0,  0],
       [ 0,  5,  4],
       [ 0,  0, 11]])

# Display the confusion matrix in a better way with matshow
confusion = confusion_matrix(y_test, y_pred)
plt.matshow(confusion, cmap='summer')
plt.colorbar()

<matplotlib.colorbar.Colorbar at 0x157642340>

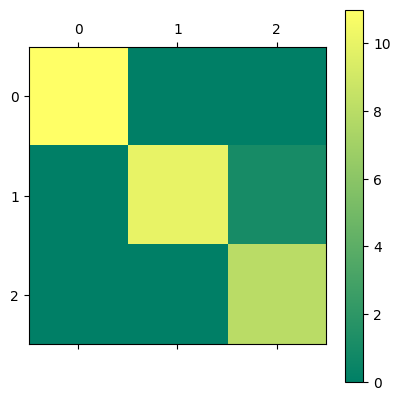
# Since RidgeClassifier is a regularized method, attempt to improve performance
# by scaling the results
scaler = StandardScaler()
scaler.fit(features)
features_Z = scaler.transform(features)

X_train, X_test, y_train, y_test = train_test_split(features_Z, labels, test_size=0.2)

ridge_classifier = RidgeClassifier()
ridge_classifier.fit(X_train, y_train)
y_pred = ridge_classifier.predict(X_test)

print(ridge_classifier.score(X_test, y_test))

confusion = confusion_matrix(y_test, y_pred)

plt.matshow(confusion, cmap='summer')
plt.colorbar()

0.9666666666666667

<matplotlib.colorbar.Colorbar at 0x157642670>

# Attempt to improve the performance with hyperparameter tuning
best_score = 0
best_alpha = None
for alpha in np.logspace(-5, 2, 5000):
    ridge_classifier = RidgeClassifier(alpha = alpha)
    ridge_classifier.fit(X_train, y_train)
    y_pred = ridge_classifier.predict(X_test)

    score = ridge_classifier.score(X_test, y_test)

    if score > best_score:
        best_score = score
        best_alpha = alpha

print('BEST ALPHA:', best_alpha)
print('BEST SCORE:', best_score)

BEST ALPHA: 1e-05
BEST SCORE: 0.9666666666666667

Potential Problems with Classification Data Sets

• There may not be clear differences between the different categories; may need a powerful classification algorithm

• Data sets may represent categorical data as text (LabelEncoder)